Tableaux et listes
Les tableaux et listes sont des structures de données fondamentales en informatique. Elles permettent de stocker et manipuler des objets en introduisant un ordre entre les éléments. Conceptuellement, les deux sont des séquences d'éléments, mais les tableaux et les listes diffèrent par leur implémentation et leur performance.
Dans cette section, nous allons voir quatre structures de données :
- Tableau statique (Array)
- Tableau dynamique (ArrayList)
- Liste simplement chaînée (Singly Linked List)
- Liste doublement chaînée (Doubly Linked List)
Tableau statique (Array)
Définition
Un tableau statique est une séquence contiguë de taille fixe.
- Taille définie à la création → pas de redimensionnement
- Accès par indice en temps constant O(1)
- Insertion/suppression au milieu nécessite la création d'un nouveau tableau ou le décalage des éléments O(n)
- Utilisé pour des données de taille connue à l'avance
Implémentation
En python, il n'existe pas de tableau statique natif, mais on peut le simuler avec une classe qui limite la modification de la taille. Voici une implémentation simplifiée d'un tableau statique :
from dataclasses import dataclass, field
@dataclass
class Array:
capacity: int
data: list = field(init=False)
def __post_init__(self):
self.data = [None] * self.capacity # None indique case vide
def get(self, index: int):
if 0 <= index < self.capacity:
return self.data[index]
raise IndexError("Index hors bornes")
def set(self, index: int, value):
if 0 <= index < self.capacity:
self.data[index] = value
else:
raise IndexError("Index hors bornes")
Ceci n'est pas très intéressant en Python, aussi bien utiliser directement le
type list qui est un tableau dynamique. Cependant, dans d'autres languages
comme C ou Java, les tableaux statiques sont natifs et peuvent être créés
directement avec une taille fixe. En C, par exemple :
int tableau[10]; // Tableau de 10 entiers
ou en Java :
int[] tableau = new int[10]; // Tableau de 10 entiers
Dans ces langages, les tableaux statiques sont homogènes (tous les éléments du même type) et la taille est fixe à la création. Cela permet une allocation mémoire contiguë et un accès rapide aux éléments par indice. De plus, l'aspect homogène permet une gestion efficace de la mémoire et des performances optimales pour les opérations d'accès et de modification.
Complexités
| Opération | Accès aléatoire | Insertion tête | Insertion fin | Insertion milieu | Suppression tête | Suppression fin | Suppression milieu | Mémoire |
|---|---|---|---|---|---|---|---|---|
| Tableau statique | O(1) | O(n) | O(n) | O(n) | O(n) | O(n) | O(n) | Faible |
Quand l’utiliser ?
- Taille connue et fixe
- Besoin d’accès aléatoire rapide
- Pas ou très peu d’insertion/suppression en cours de vie
Tableau dynamique (ArrayList)
Définition
Un tableau dynamique est un tableau redimensionnable automatiquement. Il
porte souvent le nom de ArrayList, Vector ou List dépendant du langage. En Python,
c'est le type list, en C# c'est List<T>, en Java c'est ArrayList et en C++
c'est std::vector.
La principale différence avec un tableau statique est que sa taille peut augmenter ou diminuer dynamiquement. Lorsque le tableau est plein, il est redimensionné pour doubler sa capacité, ce qui permet d'ajouter de nouveaux éléments sans avoir à créer manuellement un nouveau tableau à chaque fois.
Cela permet d'avoir un tableau qui peut croître ou rétrécir selon les besoins, tout en conservant un accès rapide aux éléments par indice. L'ajout d'un élément à la fin du tableau est généralement une opération amortie en O(1), car la redimension est rare.
Complexités
| Opération | Accès aléatoire | Insertion tête | Insertion fin | Insertion milieu | Suppression tête | Suppression fin | Suppression milieu | Mémoire |
|---|---|---|---|---|---|---|---|---|
| Tableau dynamique | O(1) | O(n) | O(1)* | O(n) | O(n) | O(1)* | O(n) | Moyen (+ redim.) |
*Insertion fin et suppression fin sont O(1) en moyenne (amorti), mais peuvent être O(n) lors d'un redimensionnement.
Quand l’utiliser ?
- Taille variable, non connue à l’avance
- Besoin fréquent d’ajouter à la fin
- Accès indexé rapide nécessaire
Visualiser le redimensionnement
Le code Python suivant permet de visualiser la croissance de la capacité
d'une liste dynamique en fonction du nombre d'éléments ajoutés. Il utilise
sys.getsizeof() pour mesurer la taille mémoire allouée et matplotlib pour
afficher un graphique de la croissance de la capacité.
import sys
import matplotlib.pyplot as plt
def plot_list_capacity(max_n: int = 2000):
"""
Mesure et affiche la croissance de la capacité mémoire d'une liste Python
jusqu'à max_n éléments.
"""
lengths = [] # nombre d'éléments dans la liste
sizes = [] # taille allouée par sys.getsizeof()
lst = []
for i in range(max_n):
lst.append(i)
lengths.append(i + 1)
sizes.append(sys.getsizeof(lst))
# Création du graphique
plt.figure(figsize=(10, 6))
plt.plot(lengths, sizes, drawstyle='steps-post')
plt.xlabel("Nombre d'éléments dans la liste")
plt.ylabel("Taille allouée (octets)")
plt.title("Croissance amortie de la capacité d'une liste Python")
plt.grid(True, linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
plot_list_capacity(max_n=2000)
Le code ci-haut devrait donner un graphique montrant comment la taille mémoire comme celui-ci
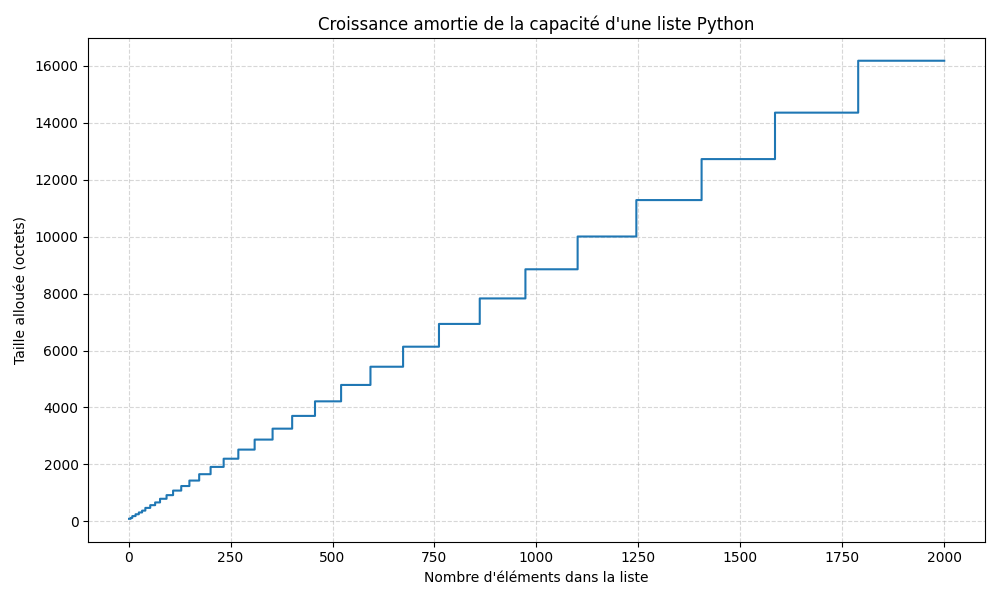 .
.
Liste simplement chaînée (Singly Linked List)
Définition
Une liste simplement chaînée (Singly Linked List) est une suite de nœuds
reliés par un pointeur next. Cela permet de stocker des éléments de manière
dynamique, sans taille fixe. L'insertion et la suppression sont rapides en tête de liste.
Par contre, l'accès par position est lent car il faut parcourir la liste depuis le début.
Implémentation
Voici une implémentation simple d'une liste simplement chaînée en Python :
from dataclasses import dataclass
from typing import Optional
@dataclass
class Node:
value: any
next: Optional['Node'] = None
@dataclass
class SinglyLinkedList:
head: Optional[Node] = None
def insert_front(self, value) -> None:
self.head = Node(value, self.head)
def get(self, index: int) -> Optional[Node]:
curr = self.head
# La présence de cette boucle indique que l'accès par index est O(n)
for _ in range(index):
if curr is None:
raise IndexError("Index hors bornes")
curr = curr.next
return curr
def set(self, index: int, value) -> None:
node = self.get(index)
if node is not None:
node.value = value
else:
raise IndexError("Index hors bornes")
Complexités
| Opération | Accès aléatoire | Insertion tête | Insertion fin | Insertion milieu | Suppression tête | Suppression fin | Suppression milieu | Mémoire |
|---|---|---|---|---|---|---|---|---|
| Liste simplement chaînée | O(n) | O(1) | O(n)* | O(n) | O(1) | O(n)* | O(n) | Pointeur simple |
*Insertion/suppression en fin est O(1) si on possède déjà le dernier nœud (par exemple si on maintient un pointeur tail), sinon O(n) car il faut parcourir la liste.
Quand l’utiliser ?
- Lorsque les noeuds sont très coûteux à recopier en mémoire
- Beaucoup d’insertion/suppression en tête
- Pas de besoin d’accès aléatoire
Liste doublement chaînée (Doubly Linked List)
Définition
Une liste doublement chaînée possède, pour chaque nœud, un pointeur next
et un pointeur prev. Elle possède les caractéristiques suivantes :
- Insertion/suppression en O(1) en tête de liste.
- Insertion/suppression en O(1) si noeud est connu.
- Traversée avant et arrière
- Accès indexé toujours O(n)
Implémentation
from dataclasses import dataclass
from typing import Optional
@dataclass
class DNode:
value: any
prev: Optional['DNode'] = None
next: Optional['DNode'] = None
@dataclass
class DoublyLinkedList:
head: Optional[DNode] = None
tail: Optional[DNode] = None
def append(self, value) -> None:
new = DNode(value, prev=self.tail)
if self.tail:
self.tail.next = new
else:
self.head = new
self.tail = new
def delete_node(self, node: DNode) -> None:
if node.prev:
node.prev.next = node.next
else:
self.head = node.next
if node.next:
node.next.prev = node.prev
else:
self.tail = node.prev
Complexités
| Opération | Accès aléatoire | Insertion tête | Insertion fin | Insertion milieu | Suppression tête | Suppression fin | Suppression milieu | Mémoire |
|---|---|---|---|---|---|---|---|---|
| Liste doublement chaînée | O(n) | O(1) | O(1)* | O(1)** | O(1) | O(1)* | O(1)** | Pointeur double |
*Insertion/suppression en tête ou en fin est O(1) si on possède déjà le nœud (par exemple via un pointeur head ou tail).
**Insertion/suppression en milieu est O(1) si on possède déjà le nœud à insérer ou à supprimer (sinon O(n) pour le trouver).
Quand l’utiliser ?
- Lorsque les noeuds sont très coûteux à recopier en mémoire
- Besoin de parcourir la liste dans les deux sens
- Suppression fréquente de nœuds intérieurs en O(1)
- Gestion de files / déques manuelles
Comparaison & Choix
| Structure | Accès aléatoire | Insertion tête | Insertion fin | Insertion milieu | Suppression tête | Suppression fin | Suppression milieu | Mémoire | Cas d’usage typiques |
|---|---|---|---|---|---|---|---|---|---|
| Tableau statique (Array) | O(1) | O(n) | O(n) | O(n) | O(n) | O(n) | O(n) | Faible | Tableaux C, buffers fixes |
| Tableau dynamique (ArrayList) | O(1) | O(n) | O(1)* | O(n) | O(n) | O(1)* | O(n) | Moyen (+ redim.) | Listes générales, pile, file |
| Liste simplement chaînée (Singly Linked) | O(n) | O(1) | O(n)* | O(n) | O(1) | O(n)* | O(n) | Pointeur simple | File FIFO, pile LIFO (stack) |
| Liste doublement chaînée (Doubly Linked) | O(n) | O(1) | O(1)* | O(1)** | O(1) | O(1)* | O(1)** | Pointeur double | Déque, navigation bidirectionnelle |
*Insertion/suppression en fin est O(1) pour les listes chaînées si on possède déjà le dernier nœud, sinon O(n). **Insertion/suppression en milieu est O(1) pour les listes doublement chaînées si on possède déjà le nœud, sinon O(n).
En résumé :
- Tableau statique (Array) : quand la taille est fixe et l’accès indexé critique.
- Tableau dynamique (ArrayList) : usage général en Python (
list), lorsque la taille varie mais que l’on veut un bon compromis accès/insertion. - Liste simplement chaînée (Singly Linked List) : pour insertions/suppressions rapides en tête, ou implémenter une file simple.
- Liste doublement chaînée (Doubly Linked List) : pour parcours bidirectionnel ou suppression rapide de n’importe quel nœud connu.